Matlab: Skripte,Funktionen und lokale Funktionen

Früher oder später stößt man darauf, dass man in .m-Dateien in Matlab nicht nur Skripte erstellen kann, sondern auch gewissen Dinge programmieren kann:

• Funktionen
• Lokale Funktionen
• Verschachtelte Funktionen
• Klassen

Warum man sich eher früher als später damit auseinander setzen sollte und was man damit so tut, erläutere ich in diesem Blog-Artikel anhand eines Beispiels.

Wenn man mit Matlab beginnt, gibt man häufig zuerst Kommandos in die Kommandozeile ein und erstellt daraus später Skripte, die man als .m-Datei speichert. Das geht eine ganze Zeit gut, doch spätestens bei komplexer werdenden Aufgaben damit scheitert, dass die Skripte nicht skalieren – also sich nicht beliebig auf größere, komplexere Probleme anpassen lassen. Typischerweise hat man einen Vektor „t“ oder „x“, den man irgendwie überschreiben will, dann tut man das aber nicht sondern schreibt nur in einen kleinen Bereich dieses Vektors und spätestens bei einer Schleife mit length(t) ist dann Schluss.

Bei den meisten Programmiersprachen versucht man daher, Globale Variablen explizit zu vermeiden, während man dies bei Matlab zu Beginn so lernt. Das hat durchaus den Vorteil, dass man einfache, eher mathematische Probleme auch schnell und einfach lösen kann, ohne sich tief mit Programmierung zu befassen. Dazu gibt es enorm viele Anwendungsfälle und genau das ist schon eine Stärke von Matlab. Ja, man kann später die Variablen in unterschiedlichen Workspaces aufteilen, aber das gehört schon zu den Fortgeschrittenen-Kenntnissen.

Fangen wir vorne an. Unser Ziel ist: Wir wollen einfach einen Graphen plotten. Aber so, dass wir das immer tun können, am Anfang, zwischendurch, ganz zum Schluss – ganz ohne mit clear all alle vorherigen Ergebnisse zu löschen.

Skripte

Sowohl Skripte als auch Funktionen werden in Matlab in .m-Dateien gespeichert. Sie unterscheiden sich lediglich durch das Schlüsselworts „function“ zu Beginn der Datei, Skripte beginnen ohne ein solches Schlüsselwort.

Ein Skript ist nichts weiter als eine Liste von Befehlen, die genau so ausgeführt werden, als würde man sie nacheinander in die Kommandozeile eingeben. Immer dann (und erst dann), wenn der letzte Befehl abgearbeitet wurde, kommt der nächste. Man kann Skripte hinter- und durcheinander starten wie man möchte, und genau dort liegt das Problem. Manchmal beginnen sie mit clear all oder clear variables, lassen aber Fenster offen und irgendwelche Objekt-Leichen bleiben übrig, die dann später stören.

Spätestens, wenn Variablen in zwei Skripten verwendet werden, die man gerne hintereinander aufrufen möchte oder die vielen Variablen der Rechnung nicht global benötigt, ist man in die Schwäche solcher einfachen Skripte gerannt (was sie nicht weniger bedeutend macht).

Ein Skript wird in einer .m-Datei gespeichert und beginnt mit irgend einer Anweisung, wie das Beispiel „beispiel_skript_1.m„:

% Dies ist ein Beispiel-Skript, bei dem zwei Variablen erstellt und dann
% grafisch dargestellt werden.
clear variables; % Alle bisher verwendeten Variablen löschen

t = 0:0.1:20; % Einen Vektor t erstellen
y = 3.*sin(t).*exp(-t/2); % y = sin(t) * e^-t 

plot(t,y)

Wenn wir dieses Skript starten, erhalten wir zwei Variablen im Workspace und ein Fenster mit einem Plot öffnet sich. Das war ja auch nichts neues.

Funktionen

Funktionen sind Programmteile, denen etwas übergeben wird (sogenannte Argumente) und die etwas zurückgeben (Rückgabewerte). Dies kann eine einzelne Variable sein, gar nichts oder, wesentlich praktischer, ein Cell-Array mit dem dann vorgegebenen Namen varargout, mit dem mehrere, verschiedene Daten zurückgegeben werden können. Das selbe gibt es auch für die übergebenen Argumente: Man kann nichts übergeben, einzelne oder mehrere Variablen oder eine ganze Liste an Variablen (varargin).

Eine Funktion wird immer mit demselben Dateiname wie ihr Funktionsname gespeichert und beginnt immer mit dem Schlüsselwort „function“ und der Definition der Schnittstelle.

Man könnte jetzt dem Lehrbuch folgen und irgend eine schöne Funktion aus der Formelsammlung in eine .m-Datei packen, aber das ist nicht der Sinn meiner Webseite. Wir bauen das Beispiel-Skript zu einer Funktion um, indem wir es etwas verändern:

function varargout = beispiel_funktion_1()
t = 0:0.1:20; % Einen Vektor t erstellen
y = 3.*sin(t).*exp(-t/2); % y = sin(t) * e^-t 

plot(t,y)
end %function

Die Funktion beginnt mit dem Schlüsselwort function und endet mit der Anweisung „end“. Das „end“ ist hier noch optional, spätestens aber bei lokalen oder verschachtelten Funktionen wird wichtig. Am besten gleich angewöhnen, denn bei if oder for tun wir das schließlich auch.

Wir geben jetzt „clear all“ im Command Window ein, schließen das Figure-Fenster öffnen die Datei beispiel_fuktion_1.m im Editor und Drücken auf die Grüne Ausführen-Schaltfläche oder drücken F5. Was man so nicht bei Funktionen erwartet, aber wir sind wie gesagt nicht im Lehrbuch.

Zur Überraschung öffnet sich wieder das Plot-Fenster aber keine Variablen sind im Workspace zu sehen. Was ist hier passiert und vor allem: Was soll das? Hat man nicht gelernt, dass man Funktionen immer durch Eingabe im Command Window starten muss? Warum geht das nun mit F5?

• Die Funktion bekommt nichts übergeben. Damit lässt sie sich wie ein Skript starten. Nur Funktionen, die Argumente benötigen, müssen mit Argumenten aufgerufen werden.
• Alle Variablen sind lokal in der Funktion und landen nicht im Workspace.
• Wir bieten varargout als Rückgabewert an. Das ist ein Sorglos-Paket, denn wir können damit variabel viele Werte und Typen übergeben. In diesem Beispiel auch einfach mal nichts, aber es schadet nicht, sich das anzugewöhnen, das benötigen wir später.
• Plot wird aus der Funktion heraus aufgerufen und tut das, was es immer tut: Es erstellt ein Fenster, eine Achse und zeichnet hinein. Das funktioniert, ist aber extrem unschön, da wir den plot nicht weiter verändern können.

Funktionen enthalten ausschließlich ihre eigenen, lokalen Variablen. Die Variablen werden nur zum Aufruf der Funktion benutzt und sind dann nicht mehr verfügbar. Möchte man die Variablen weiter nutzen, kann man sie aber ohne Probleme über varargout übergeben. Also tun wir folgendes:

• Wir erstellen ein neues Figure-Fenster und weisen den Rückgabewert des Befehls „figure“ der Variable h_fig zu. Dies nennt man ein „Handle“, darüber lassen sich diese erstellten Objekte später ansprechen. Vielleicht brauchen wir das noch, es ist jedenfalls das Ergebnis der Funktion und unser anfangs definiertes Ziel.
• Über varargout{1} geben wir dieses Figure-Handle als ersten Rückgabewert zurück.
• Weil wir es können und um varargout zu demonstrieren, geben wir die Werte von y als zweiten Rückgabewert zurück.

function varargout = beispiel_funktion_2()
t = 0:0.1:20; % Einen Vektor t erstellen
y = 3.*sin(t).*exp(-t/2); % y = sin(t) * e^-t 

h_fig = figure; % Ein neues Fenster erstellen
plot(t,y); % Den plot dort hinenzeichnen

varargout{1} = h_fig; % Handle zum Fenster
varargout{2} = y; % y-Werte
end %function

Diese Funktion können wir wieder genauso mit F5 starten wie vorher.

Und jetzt passiert etwas neues: Jedes Mal, wenn wir die Funktion starten, öffnet sich ein neues Fenster, es gibt keine globalen Variablen – außer „ans“, das ist der Rückgabwert der Funtkion. Wir bekommen im Command Window noch ein paar seltsame Dinge angezeigt: Hier sehen wir als ans das Figure-Window angezeigt wird, denn das ist auch das gewünschte Ergebnis unserer Funktion. Es müssen ja nicht immer nur Zahlen sein.

Wir können die Funktion im Command-Window (und auch von überall sonst) auch folgendermaßen aufrufen:

[fenster,ywerte] = beispiel_funktion_2();

So erhalten wir beide Werte, die wir als Elemente des varargout-Cell-Arrays mit {1} und {2} übergeben haben, von der Funktion zurück. Ein Aufruf mit

beispiel_funktion_2();

gibt das erste Element von varargout an „ans“ zurück und unterdrückt mit „;“ die Aussgabe. Nur das Fenster erhalten wir mit

fenster = beispiel_funktion_2();

und nur die y-Werte, also das zweite Element mit

[~,ywerte] = beispiel_funktion_2();

wobei die Tilde ~ einfach eine Zuweisung ins Nichts bedeutet, da wir das erste Element nicht benötigen. Man sieht hier recht schnell, wie einfach das mit varargout funktioniert. Das ist wesentlich einfacher, als sofort feste Schnittstellen festzulegen oder irgendwelche Vektoren und Matrizen ineinander zu verschachteln.

Lokale Funktionen

Lokale Funktionen sind nun zusätzliche Funktionen, die innerhalb einer Matlab-Funktion definiert werden und auch wiederum eigene, lokale Variablen haben. Eine Matlab-Funktion kann so um beliebig viele lokale Funktionen ergänzt werden. Skripte können nicht um lokale Funktionen ergänzt werden.

Wir basteln uns eine lokale Funktion in unser Beispiel, indem wir nach dieser Funktion diese in der selben .m-Datei ebenfalls per function-Schlüsselwort definieren:

function varargout = beispiel_funktion_3()
t = 0:0.1:20; % Einen Vektor t erstellen
y = lfkt3(t,2); % Die lokale Funkton mit arg1=t und arg2=2 aufrufen

h_fig = figure; % Ein neues Fenster erstellen
plot(t,y); % Den plot dort hinenzeichnen

varargout{1} = h_fig; % Handle zum Fenster
varargout{2} = y; % Y-Werte
end % function

% Eine lokale Funktion definieren
function result = lfkt3(arg1,arg2)
  tau = arg2;
  result = 3.*sin(arg1).*exp(-arg1/tau); % y = sin(t) * e^-t 
end % function lokale_anbschnitsfkt

Diese lokale Funktion hat nun, wie die eigentliche Funktion, eigene, lokale Variablen. Die einzige Schnittstelle sind die übergebenen Argumente, hier „arg1“ und „arg2“ sowie der Rückgabewert „result„. In diesem Beispiel wird die lokale Variable „tau“ definiert und durch den Funktionsaufruf lfkt1(t,2) mit „2“ als arg2 übergeben.

Keine der beiden Funktionen hat nun einen Zugriff auf die Variablen der anderen Funktion. Zugriff klingt immer, als müsse man Dinge gegeneinander schützen aber letztendlich geht es nur darum, dass man Variablen nur dort benutzt, wo man sie braucht, um Chaos zu vermeiden.

Statt in eine lokale Funktion könnte man die Funktion auch in eine eigene .m-Datei packen und dann mit zwei Dateien arbeiten, mit dem Unterschied, dass man die vorher lokale Funktion dann auch von anderen Funktionen oder Skripten aus aufrufen kann. Aber dann wäre es ja keine lokale Funktion mehr und wir hätten zwei Dateien.

Was tun, wenn wir nun nicht jedes Mal alles übergeben wollen?

Verschachtelte Funktionen

Verschachtelte Funktionen (engl. „nested functions“) oder Unterfunktionen sind Funktionen innerhalb einer Funktion, die im Gegensatz zu lokalen Funktionen, auch Zugriff auch die lokalen Variablen der eigentlichen Funktion haben. Sie lassen sich allerdings nur aus der Funktion heraus aufrufen, in die sie implementiert sind.

Wir können das vorherige Beispiel etwas ändern und die lokale Funktion in die Beispiel-Funktion schieben. Da die Funktion nfkt4 so zugriff auf die Variable tau der Funktion hat, müssen wir die Variablen nicht mehr als Argumente übergeben.

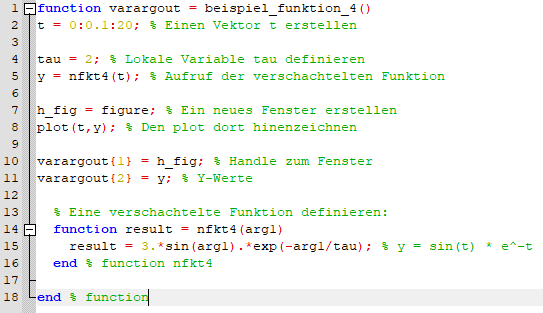
function varargout = beispiel_funktion_4()
t = 0:0.1:20; % Einen Vektor t erstellen

tau = 2; % Lokale Variable tau definieren
y = nfkt4(t); % Aufruf der verschachtelten Funktion

h_fig = figure; % Ein neues Fenster erstellen
plot(t,y); % Den plot dort hinenzeichnen

varargout{1} = h_fig; % Handle zum Fenster
varargout{2} = y; % Y-Werte

  % Eine verschachtelte Funktion definieren:
  function result = nfkt4(arg1)
    result = 3.*sin(arg1).*exp(-arg1/tau); % y = sin(t) * e^-t 
  end % function nfkt4

end % function

Die Einrückung der Funktion hat keine Auswirkung, auch der Kommentar % function nach der end-Anweisung ist optional – dies verbessert lediglich die Übersicht.

Viele Matlab-Programme sind nach einem solchen Schema programmiert, wie zum Beispiel über „GUIDE“ erstellte Benutzer-Oberflächen. Ein klarer Vorteil ist, dass ein solches Programm, wenn es in eine Funktion gekapselt ist, beliebig viele verschachtelte Unterfunktionen aufrufen kann und von jeder Stelle aus aufgerufen werden kann, da auf globale Variablen verzichtet wird.

Für Anfänger nachteilig ist der Zwang zum Debugging: Man sieht die lokalen Variablen erst, wenn man einen Breakpoint in der Funktion setzt. Das ist eigentlich völlig normal beim Programmieren, nur besteht bei Matlab zu Beginn nicht der Zwang, sich mit den Techniken außeinander zu setzen.